
|
| date | 2001-03-29:12:22 |
| Metaphysics |
A few final comments on the difference between realism and reality. Realism assumes that there is a real common plane of polarization that is shared by both photons in each pair. This has the consequence that the probability of detecting a photon depends on the cosine of the angle between the polaroid it passes through and the direction of this real plane. So for each individual photon (call them photon 1 and photon 2, which pass through polaroid 1 and polaroid 2 respectively) the probability of detection is:
where theta is the angle of orientation of the plane of polarization and theta_i is the angle of orientation of the polaroid, where i is a variable index that can be 1 or 2 depending on which polaroid we are talking about. The probability of detecting both photons in a pair is therefore equal to:
which is just the product of the individual probabilities, according to the usual rules of probability calculus. This equation was used to generate the "realism" curve shown in the previous journal entry by integrating over the angle theta using a simple Monte Carlo calculation to produce the average probability of detecting both photons in a pair as a function of the angle between the polaroids, theta1-theta2. For the mathematically minded, one way of looking at the problem with realism is that there is no way of writing the equation that describes reality:
in a form of the product of two independent functions:
and so there is no way of reproducing reality with any theory that does not posit some instantaneous interaction between the two photons. The only way the product of two functions can be made to reproduce cos(theta1-theta2) is if the "otherstuff" one of the functions depends on is itself dependent on the value of the other function, and physically this dependence appears as instantaneous communication between the photons. The communication must be instantaneous if angular momentum is conserved, and we have very good reason to believe it is. ========================= A note on conservation laws: We believe angular momentum is conserved because of No"ether's Theorem, which relates conserved quantities to symmetries of physical systems. In particular, angular momentum is associated with rotational invariance: if there is no preferred direction in the universe, then angular momentum is conserved. A great deal of effort has been invested in the past decade to look at this question with regard to the cosmic microwave background radiation, and no preferred direction has been found. Some extensions to general relativity suggest that there might be the possibility of small effects that would create a tiny preference for one direction over all others, but these effects are far too small to allow for the size of angular momentum conservation violation implied by non-instantaneous communication in photon-pair sources. It is worth nothing that correlated photon pairs are produced in one of the more common cosmological processes: electron-positron annihilation, so this question is not just a matter of a few special cases prepared by humans in laboratories. ========================= Relativity Special relativity describes the world we experience. Without writing an entire elementary textbook on SR, it's hard to appreciate how profound and inescapable it is. For the purposes of this discussion, there are a couple of essential features of the relativistic description of the world. I will try to be a good conceptualist in this description, having wallowed in the mud of realism enough for the nonce. Two of the most basic categories of experience are space and time. These are concepts abstracted from our experience of reality and of our own mental processes. Locke argues that we come to understand TIME by our awareness of the succession of ideas in our consciousness. Likewise, we come to understand SPACE by an awareness of relations between ourselves and reality. Our will causes us to interact with things--when I stand up and walk about I realize that while there is something about my experiences that stays the same, there is something that changes. As I move my feet in particular ways the world changes--some parts of my visual fields expand, others contract. I eventually learn to abstract these changes and ascribe them to changing spatial relationships between me and reality, rather than ascribing them to reality changing independently of me. That is, I recognize that the appearance of reality is relative to me, and spatial concepts such as POSITION and DISTANCE describe an important aspect of that relationship. An alternative to the analysis above, of course, is that there is a force that acts on the world such that things that I would normally describe as "far away" are getting squeezed to make them smaller, and as I move my feet in a way that I would normally say makes me approach them the strength of the force decreases and so they expand. It may even be possible to work out a consistent physics based on such a force. But it wouldn't be very parsimonious. The alternative understanding that appearances are relative to the observer is vastly simpler. Before Einstein, various odd features of electrodynamics were explained by something much like the mysterious force in the preceding paragraph. It was assumed that as objects moved more or less quickly through something called the "aether", which was supposed to permeate the universe, they were acted on by forces that caused them to shrink in the direction of motion. It turns out that Maxwell's theory of electrodynamics implied that if objects shrank this way, then time as measured by a moving observer would appear to run more slowly. Einstein recognized that the ordinary concept of "perspective" applied to motion as well as position, so that as well as the appearance of reality changing as we move around in it, it also changes when we speed up with respect to it. The laws of special relativity can be seen as a generalization of the ordinary concept of PERSPECTIVE. It is far simpler for us to understand that railway tracks appear to get closer together as the run off into the distance not because some force squeezes things far away from us, but because of our spatial relation to them. Likewise, Einstein showed that it is far easier to understand that moving objects appear foreshortened and moving clocks run slowly not because of the force of the aether acting on them, but because of the rate of change of our spatial relation to them. The consequences of this generalization of PERSPECTIVE are more important than the consequences of the ordinary kind of perspective, however. The most important consequence of special relativity is that it turns out to be impossible to define "simultaneous" for two events that are not in the same place. If two events are spatially separated, different observers will see them as happening at different times. The understand this in terms of ordinary perspective, imagine a pair of posts of different height, and two observers standing so that both observes and the posts are all in a line. To one observer, the tops of the posts may appear to line up with each other, as shown in the figure. To the other observer, one post appears to be higher than the other. To a third observer on the other side, what looks like the "tall" post to the second observer appears to be the "short" post. It's all a matter of their relative locations. 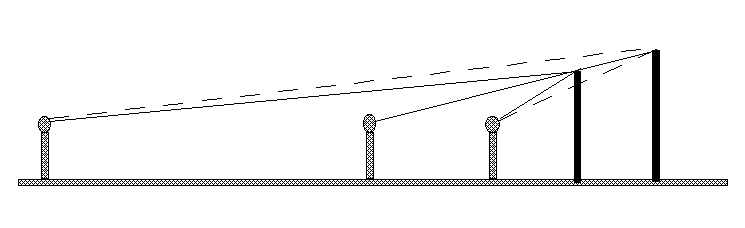 The importance for us of Einstein's extension of perspective is that when we talk about the identity of a thing, we need to specify when it is identified. And for an object that is widely extended in space we have a problem, because we would like to identify it in terms of those edges we find useful, but we cannot meaningfully define all the edges at the same time, because there is no common "instant" that applies uniformly to the entire unity bounded the the edge. The law of non-contradiction says that a thing cannot both be and not be the same thing in the same respect at the same time. For widely spatially extended things, it is not possible to specify what "at the same time" means. So how are we to identify things in terms that conform to the law of non-contradiction? This is a problem that requires further explication. Coming soon. |